【例·单选题】下列各项中，与放弃现金折扣的信用成本率呈反向变化的是（　）。
　　A.现金折扣率
　　B.折扣期
　　C.信用标准
　　D.信用期
 
『正确答案』D
『答案解析』折扣率、折扣期与放弃现金折扣的信用成本率是呈同向变化；信用期与放弃现金折扣的信用成本率呈反向变化；信用标准与放弃现金折扣的信用成本率的计算没有关系。

　　主观题主要考点及经典题解
　　【考点1】目标现金余额的确定
　　【例·计算题】假定某公司有价证券的年利率为9%，每次固定转换成本为50元，公司认为任何时候其现金余额均不能低于1 000元，又根据以往经验测算出现金余额波动的标准差为800元。
　　要求：
　　（1）指出或计算下列指标：以日为基础计算的现金机会成本、最低控制线、回归线、最高控制线；
　　（2）假设目前现金余额为20000元，此时企业应出售还是购买有价证券，金额为多少？
 
『正确答案』
　　（1）以日为基础计算的现金机会成本（有价证券日利率）＝9%÷360＝0.025%
　　最低控制线L＝1000（元）
　　　　
　　最高控制线H＝3R－2L＝3×5579－2×1000
　　 　　　　　＝14737（元）
　　（2）由于20000元大于最高控制线14737元，此时应当购买有价证券，购买的金额＝20000－5579＝14421（元）

　　【例·计算题】已知：某公司现金收支平稳，预计全年（按360天计算）现金需要量为360 000元，现金与有价证券的转换成本为每次300元，有价证券年均报酬率为6%。
　　要求：
　　（1）运用存货模式计算最佳现金持有量。
　　（2）计算最佳现金持有量下的最低现金管理相关总成本、全年现金交易成本和全年现金持有机会成本。
　　（3）计算最佳现金持有量下的全年有价证券交易次数和有价证券交易间隔期。
 
『正确答案』
　　
　　（2）最低现金管理相关总成本
　　＝60000/2×6%＋360000/60000×300＝3600（元）
　　全年现金交易成本＝360000/60000×300＝3600＝1800（元）
　　全年持有现金机会成本＝60000/2×6%＝1800（元）
　　（3）有价证券交易次数＝360000/60000＝6（次）
　　有价证券交易间隔期＝360/6＝60（天）

　　【考点2】信用政策决策
　　【例·计算题】东方公司目前采用30天按发票金额付款的信用政策。为了扩大销售，公司拟改变现有的信用政策（2/10，1/20，n/30），有关数据如下：
　　如果采用新信用政策，估计会有20%的顾客（按销售量计算，下同）在10天内付款、30%的顾客在20天内付款，其余的顾客在30天内付款。
　　假设等风险投资的最低报酬率为10%；一年按360天计算。 　　
　　
原信用政策
新信用政策
信用政策
n／30
2／10，1／20，n／30
年销售量（件）
72000
79200
年销售额（单价5元）
360 000
396 000
单位变动成本
4
4
可能发生的收账费用（元）
3000
2850
可能发生的坏账损失（元）
6000
5400
平均存货水平（件）
10000
11000
　　（1）计算信用政策改变后的收益增加；
　　（2）计算原信用政策下应收账款占用资金应计利息；
　　（3）计算新信用政策下应收账款占用资金应计利息；
　　（4）计算改变信用政策后应收账款占用资金应计利息增加；
　　（5）计算改变信用政策后存货占用资金应计利息增加；
　　（6）计算改变信用政策后收账费用增加；
　　（7）计算改变信用政策后坏账损失增加；
　　（8）计算改变信用政策后现金折扣成本增加；
　　（9）计算改变信用政策后税前损益的增加；
　　（10）根据以上计算结果，为该企业作出信用政策是否改变的决策。
 
『正确答案』
　　（1）收益增加
　　＝（79200－72000）×（5－4）＝7200（元）
　　（2）原信用政策下应收账款占用资金应计利息
　　＝360000/360×30×4/5×10%＝2400（元）
　　（3）新信用政策下：
　　平均收现期
　　＝10×20%＋20×30%＋30×50%＝23（天）
　　应收账款占用资金应计利息
　　＝396000/360×23×4/5×10%＝2024（元）
　　（4）改变信用政策后应收账款占用资金应计利息增加＝2024－2400＝－376（元）
　　（5）改变信用政策后存货占用资金应计利息增加
　　＝（11000－10000）×4×10%＝400（元）
　　（6）改变信用政策后收账费用增加
　　＝2850－3000＝－150（元）
　　（7）改变信用政策后坏账损失增加
　　＝5400－6000＝－600（元）
　　（8）改变信用政策后现金折扣成本增加
　　＝396000×20%×2%＋396000×30%×1%＝2772（元）
　　（9）改变信用政策后税前损益的增加
　　＝7200－（－376）－400－（－150）－（－600）－2772
　　＝5154（元）
　　（10）由于改变信用政策后增加了企业的税前损益，因此，企业应该采用新信用政策。

　　【考点3】存货管理
　　【例·计算题】东方公司生产中使用甲零件，全年共需耗用3600件，购入单价为9.8元，从发出定单到货物到达需要10天时间，一次订货成本72元。外购零件时可能发生延迟交货，延迟的时间和概率如下： 　　
到货延迟天数
0
1
2
3
概率
0.6
0.25
0.1
0.05
　　假设该零件的单位储存变动成本为4元，单位缺货成本为5元，一年按360天计算。建立保险储备时，最小增量为10件。
　　（1）计算甲零件的经济订货批量；
　　（2）计算最小存货成本；
　　（3）计算每年订货次数；
　　（4）计算交货期内的平均每天需要量；
　　（5）确定最合理的保险储备量和再订货点。
 
『正确答案』
　　
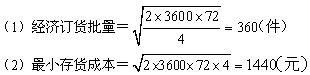
　　（3）每年订货次数＝3600/360＝10（次）
　　（4）交货期内的平均每天需要量＝3600/360＝10（件）
　　（5）如果延迟交货1天，则交货期为10＋1＝11（天），交货期内的需要量＝11×10＝110（件），概率为0.25；
　　如果延迟交货2天，则交货期为10＋2＝12（天），交货期内的需要量＝12×10＝120（件），概率为0.1；
　　如果延迟交货3天，则交货期为10＋3＝13（天），交货期内的需要量＝13×10＝130（件），概率为0.05。
　　①保险储备B＝0时
　　再订货点R＝10×10＝100（件）
　　S＝（110－100）×0.25＋（120－100）×0.1＋（130－100）×0.05＝6（件）
　　TC（S，B）＝6×5×10＋0×4＝300（元）
　　②保险储备B＝10时
　　再订货点R＝100＋10＝110（件）
　　S＝（120－110）×0.1＋（130－110）×0.05＝2（件）
　　TC（S，B）＝2×5×10＋10×4＝140（元）
　　③保险储备B＝20时
　　再订货点R＝100＋20＝120（件）
　　S＝（130－120）×0.05＝0.5（件）
　　TC（S，B）＝0.5×5×10＋20×4＝105（元）
　　④保险储备B＝30时
　　再订货点R＝100＋30＝130（件）
　　S＝0
　　TC（S，B）＝30×4＝120（元）
　　通过比较得出，最合理的保险储备为20件，再订货点为120件。

　　【考点4】放弃现金折扣的信用决策
　　【例·计算题】甲公司采购一批材料，供应商报价100万元，付款条件为：“2/10，1/20，N/90”。目前企业用于支付账款的资金需要在90天时才能周转回来，在90天内付款，只能通过银行借款解决。假设银行借款利率为5%，每年按360天计算。
　　（1）按照财务管理的理念，指出在不损害企业信誉的情况下甲公司可选择的付款方案，并计算放弃折扣的信用成本率；
　　（2）判断企业应否放弃现金折扣；
　　（3）计算不同付款方案的净收益，并选择最优的付款方案。
 
『正确答案』
　　（1）企业可选择的付款方案有：第10天付款；第20天付款；第90天付款。
　　放弃2%现金折扣的信用成本率
　　
　　放弃1%现金折扣的信用成本率
　　
　　（2）由于放弃折扣成本率高于借款利率，所以应借入银行借款以偿还货款，即不放弃现金折扣。
　　（3）第10天付款，得折扣： 100×2%＝2万元，用资98万元，借款80天，利息＝98×5%×80/360＝1.09万元，净收益＝2－1.09＝0.91万元。
　　第20天付款，得折扣1万元，用资99万元，借款70天，利息＝99×5%×70/360＝0.96万元。净收益＝1－0.96＝0.04万元。
　　应选择第10天付款方案，因为净收益最大。

　　要求：
　　（1）计算D公司2011年的营运资金数额。
 
『正确答案』营运资金＝961－575＝386（万元）

　　（2）计算D公司2011年的应收账款周转期、应付账款周转期、存货周转期以及现金周转期（为简化计算，应收账款、存货、应付账款的平均余额均以期末数据代替）。
 
『正确答案』应收账款周转期＝600/（3600/360）＝60（天）
　　应付账款周转期＝120/5＝24（天）
　　存货周转期＝150/5＝30（天）
　　现金周转期＝60＋30－24＝66（天）

　　（3）在其他条件相同的情况下，如果D公司利用供应商提供的现金折扣，则对现金周转期会产生何种影响？
 
『正确答案』如果D公司利用供应商提供的现金折扣，则应付账款周转期将会缩短，在其他条件不变的情况下，会使现金周转期延长。

　　（4）在其他条件相同的情况下，如果D公司增加存货，则对现金周转期会产生何种影响？
 
『正确答案』如果D公司增加存货，则存货周转期将会增长，在其他条件不变的情况下，会使现金周转期延长。